algemene vergelijking
We nemen een kijkje naar de vergelijking y = ax² + bx + c
paraboolvluchten.
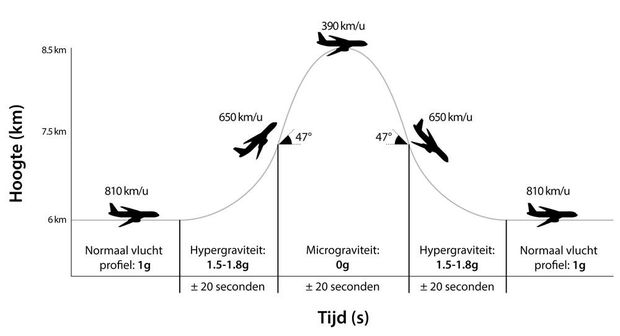
Een paraboolvlucht is een speciale vlucht dat een vliegtuig kan doen. Tijdens dit soort vlucht zal het vliegtuig met een bepaalde snelheid onder een bepaalde hoek vliegen zodat ze zero-G kunnen simuleren.
We nemen eens een kijkje naar onderstaande grafiek. We willen werken naar de vorm:
y = ax² + bx + c
Welke informatie kunnen we halen uit de grafiek die we kunnen gebruiken in de vergelijking?
We kunnen uit de grafiek enkele punten halen. Om een algemene vergelijking op te stellen zoeken we naar 3 punten.
Voor dit voorbeeld kies ik voor de punten:
A (0.2)
B (1.6)
C (5.2)
We kunnen deze coördinaten invullen in onze vergelijking.
Het punt A (0.2) ligt op de parabool
==> 2 = a.0² + b.0 + c
<=> 2 = c
Het punt B (1.6) ligt op de parabool
==> 6 = a.1² + b.1 + c
<=> 6 = a + b + c
Het punt C (5.2) ligt op de parabool
==> 2 = a.5² + b.5 + c
<=> 2 = 25a + 5b + c
Deze 3 vergelijkingen kunnen we invullen in een stelsel en vervolgens uitwerken.
uitwerking stelsel
probeer dit eerst zelf te doen, dan kan je dit gebruiken ter controle of als je even vast zit en niet meer weet wat je moet doen.
Hieruit kunnen we de vergelijking opstellen.
y = ax² + bx + c
<=> y = -x² + 5x + 2
Vragen? Contacteer me even.